- 2 Posts
- 70 Comments
Oh my Kernigan, that was stressful. Really worried about not finishing there.
Considered several approaches, the coolest of which would have been to test individual bits, propagate ‘suspicion’, etc, but it seemed too tricky.
Eventually I needed to go do something other than worry about not finishing so I started writing a validator for the adder structure. Just a couple of rules later I had found 4 faults already and managed to write automated fixups for them!
This means my solver is quite specific to my input but it can potentially be made more complete and I didn’t ‘cheat’ by hardcoding manual graph analysis.
Code
#include "common.h" /* * The approach behind part 2 was to essentially write a bunch of * validation rules for the structure of the adder, and then writing * fixups for problems it would find. That means it's likely quite * tailored to my input, but at least it's not hardcoding manual graph * analysis. */ enum { W_NULL, W_OFF, W_ON }; struct wire; struct wire { struct wire *in[2]; char name[4]; char op; /* [A]ND, [O]R, [X]OR */ int8_t val; /* W_NULL, W_OFF, W_ON */ }; static struct wire wires[320]; static struct wire *zs[46], *swapped[8]; static int nw, nsw; static struct wire * get_wire(const char *name) { int i; for (i=0; i<nw; i++) if (!strcmp(name, wires[i].name)) return &wires[i]; assert(nw < (int)LEN(wires)); assert(strlen(name) < LEN(wires[i].name)); snprintf(wires[nw].name, sizeof(wires[nw].name), "%s", name); return &wires[nw++]; } static int cmp_wires(const void *a, const void *b) { struct wire * const *wa = a; struct wire * const *wb = b; return strcmp((*wa)->name, (*wb)->name); } static int eval(struct wire *wire) { int in1,in2; if (wire->val) return wire->val == W_ON; assert(wire->in[0]); assert(wire->in[1]); in1 = eval(wire->in[0]); in2 = eval(wire->in[1]); wire->val = W_OFF + ( wire->op=='A' ? in1 && in2 : wire->op=='O' ? in1 || in2 : wire->op=='X' ? in1 != in2 : (assert(!"bad op"), -1)); return wire->val == W_ON; } static void swap(struct wire *a, struct wire *b) { struct wire tmp; //printf("swapping %s and %s\n", a->name, b->name); tmp = *a; a->op = b->op; a->in[0] = b->in[0]; a->in[1] = b->in[1]; b->op = tmp.op; b->in[0] = tmp.in[0]; b->in[1] = tmp.in[1]; assert(nsw+2 <= (int)LEN(swapped)); swapped[nsw++] = a; swapped[nsw++] = b; } static struct wire * find_z_xor(int bit) { struct wire *xy_xor; int i; for (i=0; i<nw; i++) { /* must be a XOR */ if (wires[i].op != 'X') continue; /* with an input XOR */ xy_xor = wires[i].in[0]->op == 'X' ? wires[i].in[0] : wires[i].in[1]->op == 'X' ? wires[i].in[1] : NULL; if (!xy_xor) continue; /* connected to the X and Y */ if (xy_xor->in[0]->name[0] != 'x' && xy_xor->in[0]->name[0] != 'y') continue; /* with the same bit number */ if (atoi(xy_xor->in[0]->name+1) != bit) continue; return &wires[i]; } return NULL; } static struct wire * find_xy_and(int bit) { int i; for (i=0; i<nw; i++) { /* must be AND */ if (wires[i].op != 'A') continue; /* must have XY inputs */ if ((wires[i].in[0]->name[0] != 'x' || wires[i].in[1]->name[0] != 'y') && (wires[i].in[0]->name[0] != 'y' || wires[i].in[1]->name[0] != 'x')) continue; /* with the right bit number */ if (atoi(wires[i].in[0]->name+1) != bit || atoi(wires[i].in[0]->name+1) != bit) continue; return &wires[i]; } return NULL; } static void fsck_carry_or(struct wire *or, int bit) { struct wire *wire; int i; /* both inputs must be AND; no fixup if neither */ assert( or->in[0]->op == 'A' || or->in[1]->op == 'A'); for (i=0; i<2; i++) { if (or->in[i]->op == 'A') continue; //printf("carry OR parent %s not AND\n", or->in[i]->name); /* only have fixup for the XY AND */ assert( or->in[!i]->in[0]->name[0] != 'x' && or->in[!i]->in[0]->name[0] != 'y'); wire = find_xy_and(bit); assert(wire); swap(or->in[i], wire); } } static void fsck_z(struct wire *z) { struct wire *wire, *carry_or; int bit; assert(z->name[0] == 'z'); bit = atoi(z->name+1); /* first bit is very different */ if (!bit) return; /* for the final bit, Z is the carry OR */ if (!zs[bit+1]) { /* no fixup if it isn't */ assert(z->op == 'O'); fsck_carry_or(z, bit-1); return; } /* must be a XOR */ if (z->op != 'X') { //printf("Z %s isn't XOR\n", z->name); wire = find_z_xor(bit); assert(wire); swap(z, wire); } /* bit 2 and up must have a carry OR */ if (bit > 1) { carry_or = z->in[0]->op == 'O' ? z->in[0] : z->in[1]->op == 'O' ? z->in[1] : NULL; assert(carry_or); fsck_carry_or(carry_or, bit-1); } } int main(int argc, char **argv) { struct wire *wire; char buf[64], *rest, *lf, *name1,*name2, *opstr; uint64_t p1=0; int bit, i; if (argc > 1) DISCARD(freopen(argv[1], "r", stdin)); while ((rest = fgets(buf, sizeof(buf), stdin))) { if (!strchr(buf, ':')) break; wire = get_wire(strsep(&rest, ":")); wire->val = W_OFF + atoi(rest); } while ((rest = fgets(buf, sizeof(buf), stdin))) { if ((lf = strchr(buf, '\n'))) *lf = '\0'; name1 = strsep(&rest, " "); opstr = strsep(&rest, " "); name2 = strsep(&rest, " "); strsep(&rest, " "); wire = get_wire(rest); wire->in[0] = get_wire(name1); wire->in[1] = get_wire(name2); wire->op = opstr[0]; } for (i=0; i<nw; i++) if (wires[i].name[0] == 'z') { bit = atoi(&wires[i].name[1]); assert(bit >= 0); assert(bit < (int)LEN(zs)); zs[bit] = &wires[i]; } for (i=0; i < (int)LEN(zs); i++) if (zs[i]) p1 |= (uint64_t)eval(zs[i]) << i; for (i=0; i < (int)LEN(zs); i++) if (zs[i]) fsck_z(zs[i]); qsort(swapped, nsw, sizeof(*swapped), cmp_wires); printf("24: %"PRIu64, p1); for (i=0; i<nsw; i++) printf(i ? ",%s" : " %s", swapped[i]->name); putchar('\n'); return 0; }https://codeberg.org/sjmulder/aoc/src/branch/master/2024/c/day24.c
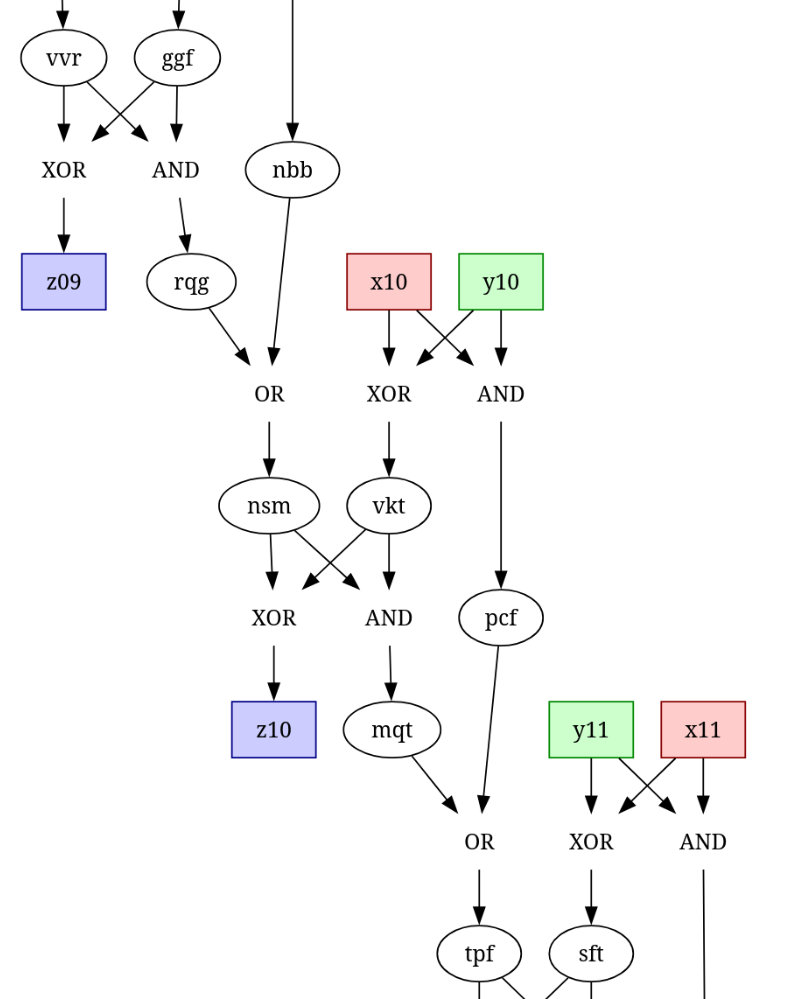
Btw, spending some time on getting Graphviz output right did make studying the structure much easier!
C
Really proud of this one! Started with with an O(n^atoms in the universe) scan which took 44s even after adding a dedup check.
But iterating on a trick to encode the deltas for the dedup check, using it to build a mapping table here, a lookup there etc brought it down to a very fast, fairly low memory, linear complexity solution!
Code
#include "common.h" #define STEPS 2000 #define NCODES (19*19*19*19) int main(int argc, char **argv) { static int8_t prices[STEPS]; static int8_t by_deltas[NCODES]; static int sums[NCODES]; uint64_t p1=0, secret; int p2=0, i; if (argc > 1) DISCARD(freopen(argv[1], "r", stdin)); while (scanf(" %"SCNu64, &secret) == 1) { memset(by_deltas, 0, sizeof(by_deltas)); for (i=0; i<STEPS; i++) { secret = (secret ^ secret << 6) & 0xFFFFFF; secret = (secret ^ secret >> 5); secret = (secret ^ secret << 11) & 0xFFFFFF; prices[i] = secret % 10; } /* * Build a deltas->price map for the buyer. Deltas are * encoded as an integer for easy indexing. Iterating * backwards ensures the stored price is the _earliest_ * occurence of that sequence. */ for (i=STEPS-1; i>=4; i--) by_deltas[ (prices[i-3] - prices[i-4] +9) *19*19*19 + (prices[i-2] - prices[i-3] +9) *19*19 + (prices[i-1] - prices[i-2] +9) *19 + (prices[i] - prices[i-1] +9) ] = prices[i]; for (i=0; i<NCODES; i++) sums[i] += by_deltas[i]; p1 += secret; } for (i=0; i<NCODES; i++) p2 = MAX(p2, sums[i]); printf("22: %"PRIu64" %d\n", p1, p2); return 0; }day22 0m00.04s realhttps://codeberg.org/sjmulder/aoc/src/branch/master/2024/c/day22.c
C
Graph problems are not my cake but this one I could work out: recursively iterate unique combination of adjacent nodes. Performance benefits from using a basic, int-indexed adjacency matrix.
Fast enough on my 2015 PC:
day23 0:00.05 1644 Kb 0+143 faultsCode
#include "common.h" #define VZ 520 /* max no. vertices */ #define SZ 32 /* max set size */ static char names[VZ][3]; static char adj[VZ][VZ]; static int nvert; static int to_id(const char *name) { int i; for (i=0; i<nvert; i++) if (!strcmp(name, names[i])) return i; assert(nvert < VZ); assert(strlen(name) < LEN(*names)); snprintf(names[nvert++], sizeof(*names), "%s", name); return i; } static int cmp_id(const void *a, const void *b) { return strcmp(names[*(int*)a], names[*(int*)b]); } /* * Construct all unique combinations of nodes, with every extension, * confirm they're all connected. Essentally this but recursive: * * for (a=0; a<nvert; a++) * for (b=a+1; b<nvert; b++) * for (c=b+1; c<nvert; c++) * ... * * Note the inner loops continue forward from the point of the outside * loop, avoiding duplicate combinations. * * 'set' and 'best' are arrays of size SZ, length 'sz' and 'bz'. 'set' * is the current working state; 'best' is a copy of the longest known * set. */ static int max_set(int *set, int sz, int *best, int bz) { int bz1, v,i; assert(sz < SZ); /* for each potential candidate */ for (v = sz ? set[sz-1]+1 : 0; v < nvert; v++) { /* adjacent to all in current set? */ for (i=0; i<sz && adj[set[i]][v]; i++) ; if (i != sz) continue; /* recur and update 'best size' if needed */ set[sz] = v; if (bz < (bz1 = max_set(set, sz+1, best, bz))) bz = bz1; } /* store longest known set in 'best' */ if (sz > bz) memcpy(best, set, (bz = sz) * sizeof(*best)); return bz; } int main(int argc, char **argv) { static int set[SZ], best[SZ]; char buf[8]; int p1=0, a,b,c, i, bz; if (argc > 1) DISCARD(freopen(argv[1], "r", stdin)); while (fgets(buf, sizeof(buf), stdin)) { assert(strlen(buf) >= 5); buf[2] = buf[5] = '\0'; a = to_id(buf); b = to_id(buf+3); adj[a][b] = adj[b][a] = 1; } for (a=0; a<nvert; a++) for (b=a+1; b<nvert; b++) for (c=b+1; c<nvert; c++) p1 += adj[a][b] && adj[a][c] && adj[b][c] && ( names[a][0] == 't' || names[b][0] == 't' || names[c][0] == 't'); printf("23: %d ", p1); bz = max_set(set, 0, best, 0); qsort(best, bz, sizeof(*best), cmp_id); for (i=0; i<bz; i++) printf(i ? ",%s" : "%s", names[best[i]]); putchar('\n'); return 0; }https://codeberg.org/sjmulder/aoc/src/branch/master/2024/c/day23.c

 1·6 months ago
1·6 months agoFinally got this one done very late last night!
I kept getting stuck reasoning about the recursion here. For some reason I got myself convinced that after a move, the state of the ‘upper’ dpads could make it more advantageous to pick one followup move over another - i.e. steps aren’t independent.
It took a bunch of manually working through sequences to convince myself that, after every move, every dpad above it would be on A. With that, it’s ‘just’ recursive pathfinding for independent moves.
Since there are relatively few types of moves needed on the dpad, I just sketched them out and wrote the routes in code directly (up to two options per move, e.g. left,up or up,left).
Code
#include "common.h" static int64_t dpmem[26][8][2]; enum {NW,NN,NE,EE,SE,SS,SW,WW}; /* * We can sufficiently describe npad/dpad movements as: "move N x, N y, * then press A N times" (a 'move'). It's never faster to take a detour. * After pressing A on one dpad, dpads on all levels above will also be * on A, so these moves can be considered in isolation. * * This function gives the cost of executing a move with the dpad in * direction 'd' at level 'l', excluding the A presses for actually * tapping the selected directions, but including returning the cursor * back to the A button. * * E.g., moving 2 up and 3 left (NW), the steps could be <AAv<AAA>>^. * Excluding the A presses, that's 6 steps. Pulling out the A presses * lets us drop the dx and dy arguments and simplify the memoization. * They're easily calculated: it's |dx|+|dy|. * * The gaps present a problem: picking the lowest-cost option (e.g. * left-then-up vs. up-then-left) may cause us to cross a gap. The * "mind the gap" argument 'mtg' must be set to 1 if-and-only-if there * is such potential, e.g. a move from < to ^ on the dpad (up,right * crosses the gap) or a move from A to 1 on the npad (left,up crosses * the gap). With the flag set, these orderings will be avoided. */ static int64_t dp(int d, int mtg, int l) { int64_t ret, alt=INT64_MAX; if (l<=0) return 0; assert(l >= 0); assert(l < (int)LEN(dpmem)); assert(mtg==0 || mtg==1); if ((ret = dpmem[l][d][mtg])) return ret; /* routes avoiding gaps where necessary */ ret = d==SE ? 1+dp(SS,0,l-1) + 1+dp(WW,0,l-1) + 2+dp(SE,0,l-1) : d==SW ? 2+dp(SW,0,l-1) + 1+dp(WW,0,l-1) + 3+dp(NE,1,l-1) : d==SS ? 2+dp(SW,0,l-1) + 2+dp(NE,0,l-1) : d==NE ? 1+dp(SS,0,l-1) + 2+dp(NW,0,l-1) + 1+dp(EE,0,l-1) : d==NW ? 1+dp(WW,0,l-1) + 2+dp(SW,1,l-1) + 3+dp(NE,1,l-1) : d==NN ? 1+dp(WW,0,l-1) + 1+dp(EE,0,l-1) : d==EE ? 1+dp(SS,0,l-1) + 1+dp(NN,0,l-1) : d==WW ? 3+dp(SW,1,l-1) + 3+dp(NE,1,l-1) : (assert(!"bad dir"), -1); /* alternatives crossing the gaps */ alt = mtg ? INT64_MAX : d==SE ? 2+dp(SW,0,l-1) + 1+dp(EE,0,l-1) + 1+dp(NN,0,l-1) : d==SW ? 3+dp(SW,1,l-1) + 1+dp(EE,0,l-1) + 2+dp(NE,0,l-1) : d==NE ? 1+dp(WW,0,l-1) + 2+dp(SE,0,l-1) + 1+dp(NN,0,l-1) : d==NW ? 3+dp(SW,1,l-1) + 2+dp(NE,1,l-1) + 1+dp(EE,0,l-1) : INT64_MAX; return dpmem[l][d][mtg] = MIN(ret, alt); } static int64_t npcost(const char *s, int lv) { int64_t cost=0; int x=2,y=3, x1,y1, mtg, dir; for (; *s == 'A' || (*s >= '0' && *s <= '9'); s++) { x1 = *s=='A' ? 2 : *s=='0' ? 1 : 2-(9-*s+'0') % 3; y1 = *s=='A' ? 3 : *s=='0' ? 3 : (9-*s+'0') / 3; /* potentially crossing a gap? */ mtg = (x==0 && y1==3) || (x1==0 && y==3); dir = y1>y ? (x1>x ? SE : x1<x ? SW : SS) : y1<y ? (x1>x ? NE : x1<x ? NW : NN) : (x1>x ? EE : x1<x ? WW : 0); cost += dp(dir, mtg, lv) + abs(x1-x) + abs(y1-y) +1; x = x1; y = y1; } return cost; } int main(int argc, char **argv) { char buf[8]; int digits; int64_t p1=0,p2=0; if (argc > 1) DISCARD(freopen(argv[1], "r", stdin)); while (fgets(buf, sizeof(buf), stdin)) { digits = atoi(buf); p1 += digits * npcost(buf, 2); p2 += digits * npcost(buf, 25); } printf("21: %"PRId64" %"PRId64"\n", p1, p2); return 0; }https://codeberg.org/sjmulder/aoc/src/branch/master/2024/c/day21.c

 2·6 months ago
2·6 months agoC
Note to self: reread the puzzle after waking up properly! I initially wrote a great solution for the wrong question (pathfinding with a given number of allowed jumps).
For the actual question, a bit boring but flood fill plus some array iteration saved the day again. Find the cost for every open tile with flood fill, then for each position and offset combination, see if that jump yields a lower cost at the destination.
For arbitrary inputs this would require eliminating the non-optimal paths, but the one path covered all open tiles.
Code
#include "common.h" #define GB 2 /* safety border on X/Y plane */ #define GZ (GB+141+2+GB) static char G[GZ][GZ]; /* grid */ static int C[GZ][GZ]; /* costs */ static int sx,sy, ex,ey; /* start, end pos */ static void flood(int x, int y) { int lo = INT_MAX; if (x<1 || x>=GZ-1 || y<1 || y>=GZ-1 || G[y][x]!='.') return; if (C[y-1][x]) lo = MIN(lo, C[y-1][x]+1); if (C[y+1][x]) lo = MIN(lo, C[y+1][x]+1); if (C[y][x-1]) lo = MIN(lo, C[y][x-1]+1); if (C[y][x+1]) lo = MIN(lo, C[y][x+1]+1); if (lo != INT_MAX && (!C[y][x] || lo < C[y][x])) { C[y][x] = lo; flood(x, y-1); flood(x-1, y); flood(x, y+1); flood(x+1, y); } } static int count_shortcuts(int lim, int min) { int acc=0, x,y, dx,dy; for (y=GB; y<GZ-GB; y++) for (x=GB; x<GZ-GB; x++) for (dy = -lim; dy <= lim; dy++) for (dx = abs(dy)-lim; dx <= lim-abs(dy); dx++) acc += x+dx >= 0 && x+dx < GZ && y+dy >= 0 && y+dy < GZ && C[y][x] && C[y][x]+abs(dx)+abs(dy) <= C[y+dy][x+dx]-min; return acc; } int main(int argc, char **argv) { int x,y; if (argc > 1) DISCARD(freopen(argv[1], "r", stdin)); for (y=2; fgets(G[y]+GB, GZ-GB*2, stdin); y++) assert(y < GZ-3); for (y=GB; y<GZ-GB; y++) for (x=GB; x<GZ-GB; x++) if (G[y][x] == 'S') { G[y][x]='.'; sx=x; sy=y; } else if (G[y][x] == 'E') { G[y][x]='.'; ex=x; ey=y; } C[sy][sx] = 1; flood(sx, sy-1); flood(sx-1, sy); flood(sx, sy+1); flood(sx+1, sy); printf("20: %d %d\n", count_shortcuts(2, 100), count_shortcuts(20, 100)); return 0; }https://codeberg.org/sjmulder/aoc/src/branch/master/2024/c/day20.c

 2·6 months ago
2·6 months agoCertainly more generic and less prone to user error too. Indeed dealing with hash maps or any advanced data structure is a pain with C, this is where generics or templates really shine, especially if you have control over lifetime aspects as you do with C++ or Rust (e.g. moves, lvalue references, constness, etc).
I think I saw the same! At first I thought it requires pathfinding to see what nodes are connected to the wall, but then someone pointed at disjoint sets and just a glance at Wikipedia made it click right away. What an ingeniously simple but useful data structure! Maybe I’ll reimplement my solution with that - mostly as an exercise for disjoint sets and finding a convenient representation for that in C.

 3·6 months ago
3·6 months agoThat does mean that if two or more strings end with the same substring, you’d recalculate those substrings?
I hadn’t really considered that, but yes. I’m inclined to think that replacing hash table lookups with plain array indexing (which this allows) outweighs that downside but I’m not sure. Indeed 120ms is pretty damn fast!

 3·6 months ago
3·6 months agoLovely! This is nicer than my memoized recursion. DP remains hard to wrap my head around even though I often apply it by accident.
until I tried matching from right to left instead :3
My intuition nudged me there but I couldn’t reason how that would change things. You still have to test the remaining string, and its remaining string, backtrack, etc right?

 2·6 months ago
2·6 months agoI don’t know much about Rust but I assume the
HashMap<String, i64>requires hashing on insertion and lookup, right? I realized that, for every design, all the strings you’ll see are substrings of that design from different starting positions, so I made my lookup tableint pos -> int count. The table is reset after every design.

 1·6 months ago
1·6 months agoAwesome! I understood the idea behind the binary search but thought it wasn’t a good fit for the flood fill. As opposed to something like A* it will give you reachability and cost for every cell (at a cost), but that’s no use when you do repeated searches that are only meant to find a single path. So I was very happy with your suggestion, it fits better with the strengths.
“Virtually instant” btw is measured 0.00 by
time. I like it when things are fast but I also prefer simper approaches (that is: loops and arrays) over the really optimized fast stuff. People do really amazing things but the really clever algorithms lean on optimized generic data structures that C lacks. It’s fun though to see how far you can drive loops and arrays! Perhaps next year I’ll pick a compiled language with a rich data structure library and really focus on effectively applying good algorithms and appropriate data structures.Btw how do you measure performance? I see a lot of people including timing things in their programs but I can’t be bothered. Some people also exclude parsing - which wouldn’t work for me because I try to process the input immediately, if possible.
C
Interestingly part 1 already defied a naive approach. It was fun thinking of a way to memoize without hash tables.
Code
#include "common.h" static char *pats[480]; static int lens[480]; int np; /* memoized for 's' by mem[off], 0 = unknown, >0 = value+1 */ static int64_t recur(char *s, int off, int64_t *mem) { int64_t acc=0; int i; if (!s[off]) return 1; if (mem[off]) return mem[off]-1; for (i=0; i<np; i++) if (!strncmp(s+off, pats[i], lens[i])) acc += recur(s, off+lens[i], mem); mem[off] = acc+1; return acc; } int main(int argc, char **argv) { static char patbuf[3200], design[64]; int64_t p1=0,p2=0, mem[64], n; char *rest, *lf; if (argc > 1) DISCARD(freopen(argv[1], "r", stdin)); rest = fgets(patbuf, sizeof(patbuf), stdin); for (; (pats[np] = strsep(&rest, ",")); np++) { while (isspace(pats[np][0])) pats[np]++; /* skip spaces */ if ((lf = strchr(pats[np], '\n'))) *lf = '\0'; /* trim trailing \n */ lens[np] = strlen(pats[np]); assert(np+1 < (int)LEN(pats)); } while (scanf(" %63s", design) == 1) { memset(mem, 0, sizeof(mem)); n = recur(design, 0, mem); p1 += n >0; p2 += n; } printf("19: %"PRId64" %"PRId64"\n", p1, p2); return 0; }https://codeberg.org/sjmulder/aoc/src/branch/master/2024/c/day19.c
Zee
Also a port to my cursed Dutch dialect of C, Zee:
Code
#ingesloten "zee.kop" #ingesloten "algemeen.kop" besloten letterverwijzing patronen[480]; besloten getal lengtes[480]; getal patroonsom; besloten zeer groot getal afdaling( letterverwijzing tekst, getal startpositie, zeergrootgetalreeksverwijzing onthouden) { zeer groot getal deelsom=0; getal sortering, teller; tenzij (tekst[startpositie]) lever 1; mits (onthouden[startpositie]) lever onthouden[startpositie]-1; voor (teller=0; teller < patroonsom; teller++) { sortering = tekstdeelvergelijking( tekst + startpositie, patronen[teller], lengtes[teller]); mits (sortering == 0) { deelsom += afdaling( tekst, startpositie + lengtes[teller], onthouden); } } onthouden[startpositie] = deelsom+1; lever deelsom; } getal aanvang( getal parametersom, letterverwijzingsreeksverwijzing parameters) { blijvende letter patroonruimte[3200]; blijvende letter ontwerp[64]; zeer groot getal deel1=0, aantal; zeer groot getal deel2=0, onthouden[64]; letterverwijzing rest; letterverwijzing regeleinde; mits (parametersom > 1) VERWERP(heropen(parameters[1], "r", standaardinvoer)); rest = geefregel(patroonruimte, grootte(patroonruimte), standaardinvoer); voor (; ; patroonsom++) { verzeker(patroonsom+1 < (getal)LENGTE(patronen)); patronen[patroonsom] = tekstsplitsing(naar rest, ","); mits (patronen[patroonsom] == NIETS) klaar; zolang (iswitruimte(patronen[patroonsom][0])) patronen[patroonsom]++; mits ((regeleinde = zoekletter(patronen[patroonsom], '\n'))) volg regeleinde = '\0'; lengtes[patroonsom] = tekstlengte(patronen[patroonsom]); } zolang (invorm(" %63s", ontwerp) == 1) { overschrijf(onthouden, 0, grootte(onthouden)); aantal = afdaling(ontwerp, 0, onthouden); deel1 += aantal >0; deel2 += aantal; } uitvorm("19: %"GEEFZGG" %"GEEFZGG"\n", deel1, deel2); lever 0; }
Thanks, that’s exactly the sort of insight that I was too tired to have at that point 😅
The other thing I had to change was to make it recursive rather than iterating over the full grid - the latter is fast for large update, but very wasteful for local updates, like removing the points. Virtually instant now!
Code
#include "common.h" #define SAMPLE 0 #define PTZ 3600 #define GZ (SAMPLE ? 9 : 73) #define P1STEP (SAMPLE ? 12 : 1024) #define CORR -1 static int g[GZ][GZ]; static void flood(int x, int y) { int lo=INT_MAX; if (x <= 0 || x >= GZ-1 || y <= 0 || y >= GZ-1 || g[y][x] == CORR) return; if (g[y-1][x] > 0) lo = MIN(lo, g[y-1][x] +1); if (g[y+1][x] > 0) lo = MIN(lo, g[y+1][x] +1); if (g[y][x-1] > 0) lo = MIN(lo, g[y][x-1] +1); if (g[y][x+1] > 0) lo = MIN(lo, g[y][x+1] +1); if (lo != INT_MAX && (!g[y][x] || g[y][x] > lo)) { g[y][x] = lo; flood(x, y-1); flood(x, y+1); flood(x-1, y); flood(x+1, y); } } int main(int argc, char **argv) { static int xs[PTZ], ys[PTZ]; static char p2[32]; int p1=0, npt=0, i; if (argc > 1) DISCARD(freopen(argv[1], "r", stdin)); for (i=0; i<GZ; i++) g[0][i] = g[GZ-1][i] = g[i][0] = g[i][GZ-1] = CORR; for (npt=0; npt<PTZ && scanf(" %d,%d", xs+npt, ys+npt)==2; npt++) { assert(xs[npt] >= 0); assert(xs[npt] < GZ-2); assert(ys[npt] >= 0); assert(ys[npt] < GZ-2); } assert(npt < PTZ); for (i=0; i<npt; i++) g[ys[i]+1][xs[i]+1] = CORR; g[1][1] = 1; flood(2, 1); flood(1, 2); for (i=npt-1; i >= P1STEP; i--) { g[ys[i]+1][xs[i]+1] = 0; flood(xs[i]+1, ys[i]+1); if (!p2[0] && g[GZ-2][GZ-2] > 0) snprintf(p2, sizeof(p2), "%d,%d", xs[i],ys[i]); } p1 = g[GZ-2][GZ-2]-1; printf("18: %d %s\n", p1, p2); return 0; }

 1·6 months ago
1·6 months agoC
Flood fill for part 1. Little tired so for part 2 I just retry the flood fill every step. Slow by C standards (2s) but I’ll let it brew and come back to it later.
Code
#include "common.h" #define SAMPLE 0 #define GZ (SAMPLE ? 9 : 73) #define NCORR (SAMPLE ? 12 : 1024) #define CORR -1 int g[GZ][GZ]; static void flood(void) { int x,y, dirty=1, lo; for (y=1; y<GZ-1; y++) for (x=1; x<GZ-1; x++) if (g[y][x] > 1) g[y][x] = 0; while (dirty) { dirty = 0; for (y=1; y<GZ-1; y++) for (x=1; x<GZ-1; x++) { if (g[y][x] == CORR) continue; lo = INT_MAX; if (g[y-1][x] > 0) lo = MIN(lo, g[y-1][x]); if (g[y+1][x] > 0) lo = MIN(lo, g[y+1][x]); if (g[y][x-1] > 0) lo = MIN(lo, g[y][x-1]); if (g[y][x+1] > 0) lo = MIN(lo, g[y][x+1]); if (lo != INT_MAX && (!g[y][x] || g[y][x]>lo+1)) { dirty=1; g[y][x] = lo+1; } } } } int main(int argc, char **argv) { int p1=0, x,y, i; if (argc > 1) DISCARD(freopen(argv[1], "r", stdin)); for (i=0; i<GZ; i++) g[0][i] = g[GZ-1][i] = g[i][0] = g[i][GZ-1] = CORR; g[1][1] = 1; for (i=0; scanf(" %d,%d", &x, &y) == 2; i++) { assert(x >= 0); assert(x < GZ-2); assert(y >= 0); assert(y < GZ-2); g[y+1][x+1] = CORR; flood(); if (i==NCORR-1) p1 = g[GZ-2][GZ-2]-1; if (g[GZ-2][GZ-2] <= 0) { printf("18: %d %d,%d\n", p1, x,y); return 0; } } assert(!"no solution"); return -1; }

 2·6 months ago
2·6 months agoC
Was looking forward to a VM! Really took my leisure for part 1, writing a disassembler, tracing, all pretty.
Part 2 reminded me of 2021 day 24 where we also had to reverse an input. It’s been on my mind recently and I was thinking if there would be a way to backfeed an output through a program, yielding a representation like: “the input plus 3498 is a multiple of 40, and divisible by a number that’s 5 mod 8” (considering lossy functions like modulo and integer division).
Today’s input didn’t lend itself to that, however, but analysing it having the solution ‘click’ was very satisfying.
Code
#include "common.h" #define MEMZ 32 #define OUTZ 32 #define BUFZ 64 enum { ADV, BXL, BST, JNZ, BXC, OUT, BDV, CDV }; struct vm { int64_t mem[MEMZ]; int nm, pc; int64_t out[OUTZ]; int no; int64_t a,b,c; } vm; /* returns 0 if halted, 1 otherwise */ static int step(void) { int64_t op, ar, ac; /* operator, lit. arg, combo arg */ assert(vm.pc >= 0); assert(vm.pc+2 <= MEMZ); if (vm.pc >= vm.nm) return 0; op = vm.mem[vm.pc++]; ar = vm.mem[vm.pc++]; ac = ar==4 ? vm.a : ar==5 ? vm.b : ar==6 ? vm.c : ar; switch (op) { case ADV: vm.a = vm.a >> ac; break; case BDV: vm.b = vm.a >> ac; break; case CDV: vm.c = vm.a >> ac; break; case BXL: vm.b = vm.b ^ ar; break; case BXC: vm.b = vm.b ^ vm.c; break; case BST: vm.b = ac % 8; break; case JNZ: if (vm.a) vm.pc = ar; break; case OUT: assert(vm.no < OUTZ); vm.out[vm.no++] = ac%8; break; default: assert(!"invalid opcode"); return 0; } return 1; } static int64_t recur_p2(int64_t a0, int pos) { int64_t a, i; /* * The code in the input uses up to 7 low bits of the A register * to produce a single number, then chops off the low 3 bits and * continues. * * That means bits above the current triplet influence what * number it generates, but bits below don't. To generate a * desired sequence then, we append, not prepend, candidate * triplets. * * We may end up in a situation where, given the prefix found * for the numbers so far, no triplet yields the desired next * number. Then we have to backtrack and find another prefix, * hence the recursion. */ if (pos >= vm.nm) return a0 >> 3; for (i=0; i<8; i++) { vm.a=a= a0+i; vm.b=vm.c=vm.pc=vm.no= 0; while (step() && !vm.no) ; if (vm.no && vm.out[0] == vm.mem[vm.nm-pos-1]) if ((a = recur_p2(a << 3, pos+1))) return a; } return 0; } int main(int argc, char **argv) { char b[BUFZ], *tok, *rest; int i; if (argc > 1) DISCARD(freopen(argv[1], "r", stdin)); fgets(b, BUFZ, stdin); sscanf(b, "Register A: %lld", &vm.a); fgets(b, BUFZ, stdin); sscanf(b, "Register B: %lld", &vm.b); fgets(b, BUFZ, stdin); sscanf(b, "Register C: %lld", &vm.c); fgets(b, BUFZ, stdin); assert(vm.b == 0); /* assumption for part 2 */ assert(vm.c == 0); rest = fgets(b, sizeof(b), stdin); strsep(&rest, ":"); while ((tok = strsep(&rest, ","))) { assert(vm.nm < MEMZ); vm.mem[vm.nm++] = atoll(tok); } while (step()) ; for (i=0; i<vm.no; i++) printf(i ? ",%lld" : "17: %lld", vm.out[i]); printf(" %lld\n", recur_p2(0, 0)); return 0; }
C
Yay more grids! Seemed like prime Dijkstra or A* material but I went with an iterative approach instead!
I keep an array cost[y][x][dir], which is seeded at 1 for the starting location and direction. Then I keep going over the array, seeing if any valid move (step or turn) would yield to a lower best-known-cost for this state. It ends when a pass does not yield changes.
This leaves us with the best-known-costs for every reachable state in the array, including the end cell (bit we have to take the min() of the four directions).
Part 2 was interesting: I just happend to have written a dead end pruning function for part 1 and part 2 is, really, dead-end pruning for the cost map: remove any suboptimal step, keep doing so, and you end up with only the optimal steps. ‘Suboptimal’ here is a move that yields a higher total cost than the best-known-cost for that state.
It’s fast enough too on my 2015 i5:
day16 0:00.05 1656 Kb 0+242 faultsCode
#include "common.h" #define GZ 145 enum {NN, EE, SS, WW}; static const int dx[]={0,1,0,-1}, dy[]={-1,0,1,0}; static char g[GZ][GZ]; /* with 1 tile border */ static int cost[GZ][GZ][4]; /* per direction, starts at 1, 0=no info */ static int traversible(char c) { return c=='.' || c=='S' || c=='E'; } static int minat(int x, int y) { int acc=0, d; for (d=0; d<4; d++) if (cost[y][x][d] && (!acc || cost[y][x][d] < acc)) acc = cost[y][x][d]; return acc; } static int count_exits(int x, int y) { int acc=0, i; assert(x>0); assert(x<GZ-1); assert(y>0); assert(y<GZ-1); for (i=0; i<4; i++) acc += traversible(g[y+dy[i]][x+dx[i]]); return acc; } /* remove all dead ends */ static void prune_dead(void) { int dirty=1, x,y; while (dirty) { dirty = 0; for (y=1; y<GZ-1; y++) for (x=1; x<GZ-1; x++) if (g[y][x]=='.' && count_exits(x,y) < 2) { dirty = 1; g[y][x] = '#'; } } } /* remove all dead ends from cost[], leaves only optimal paths */ static void prune_subopt(void) { int dirty=1, x,y,d; while (dirty) { dirty = 0; for (y=1; y<GZ-1; y++) for (x=1; x<GZ-1; x++) for (d=0; d<4; d++) { if (!cost[y][x][d]) continue; if (g[y][x]=='E') { if (cost[y][x][d] != minat(x,y)) { dirty = 1; cost[y][x][d] = 0; } continue; } if (cost[y][x][d]+1 > cost[y+dy[d]][x+dx[d]][d] && cost[y][x][d]+1000 > cost[y][x][(d+1)%4] && cost[y][x][d]+1000 > cost[y][x][(d+3)%4]) { dirty = 1; cost[y][x][d] = 0; } } } } static void propagate_costs(void) { int dirty=1, cost1, x,y,d; while (dirty) { dirty = 0; for (y=1; y<GZ-1; y++) for (x=1; x<GZ-1; x++) for (d=0; d<4; d++) { if (!traversible(g[y][x])) continue; /* from back */ if ((cost1 = cost[y-dy[d]][x-dx[d]][d]) && (cost1+1 < cost[y][x][d] || !cost[y][x][d])) { dirty = 1; cost[y][x][d] = cost1+1; } /* from right */ if ((cost1 = cost[y][x][(d+1)%4]) && (cost1+1000 < cost[y][x][d] || !cost[y][x][d])) { dirty = 1; cost[y][x][d] = cost1+1000; } /* from left */ if ((cost1 = cost[y][x][(d+3)%4]) && (cost1+1000 < cost[y][x][d] || !cost[y][x][d])) { dirty = 1; cost[y][x][d] = cost1+1000; } } } } int main(int argc, char **argv) { int p1=0,p2=0, sx=0,sy=0, ex=0,ey=0, x,y; char *p; if (argc > 1) DISCARD(freopen(argv[1], "r", stdin)); for (y=1; fgets(g[y]+1, GZ-1, stdin); y++) { if ((p = strchr(g[y]+1, 'S'))) { sy=y; sx=p-g[y]; } if ((p = strchr(g[y]+1, 'E'))) { ey=y; ex=p-g[y]; } assert(y+1 < GZ-1); } cost[sy][sx][EE] = 1; prune_dead(); propagate_costs(); prune_subopt(); p1 = minat(ex, ey) -1; /* costs[] values start at 1! */ for (y=1; y<GZ-1; y++) for (x=1; x<GZ-1; x++) p2 += minat(x,y) > 0; printf("16: %d %d\n", p1, p2); return 0; }

 1·6 months ago
1·6 months agoC
3h+ train ride back home from weekend trip but a little tired and not feeling it much. Finished part 1, saw that part 2 was fiddly programming, left it there.
Finally hacked together something before bed. The part 2 twist required rewriting the push function to be recursive but also a little care and debugging to get that right. Cleaned it up over lunch, happy enough with the solution now!
Code
#include "common.h" #define GW 104 #define GH 52 struct world { char g[GH][GW]; int px,py; }; static int can_clear(struct world *w, int x, int y, int dx, int dy) { assert(x>=0); assert(x<GW); assert(y>=0); assert(y<GH); assert((dx && !dy) || (dy && !dx)); return (x+dx >= 0 || x+dx < GW) && (y+dy >= 0 || y+dy < GW) && (w->g[y][x] == '.' || ( w->g[y][x] != '#' && can_clear(w, x+dx,y+dy, dx,dy) && (!dy || w->g[y][x]!='[' || can_clear(w, x+1,y+dy, 0,dy)) && (!dy || w->g[y][x]!=']' || can_clear(w, x-1,y, 0,dy)) && (!dy || w->g[y][x]!=']' || can_clear(w, x-1,y+dy, 0,dy)))); } /* check can_clear() first! */ static void clear(struct world *w, int x, int y, int dx, int dy) { assert(x>=0); assert(x<GW); assert(x+dx>=0); assert(x+dx<GW); assert(y>=0); assert(y<GH); assert(y+dy>=0); assert(y+dy<GH); if (w->g[y][x] == '.') return; if (dy && w->g[y][x] == ']') { clear(w, x-1,y, dx,dy); return; } if (dy && w->g[y][x] == '[') { clear(w, x+1,y+dy, dx,dy); w->g[y+dy][x+dx+1] = ']'; w->g[y][x+1] = '.'; } clear(w, x+dx,y+dy, dx,dy); w->g[y+dy][x+dx] = w->g[y][x]; w->g[y][x] = '.'; } static void move(struct world *w, int dx, int dy) { if (can_clear(w, w->px+dx, w->py+dy, dx,dy)) { clear(w, w->px+dx, w->py+dy, dx,dy); w->px += dx; w->py += dy; } } static int score(struct world *w) { int acc=0, x,y; for (y=0; y<GH && w->g[y][0]; y++) for (x=0; x<GW && w->g[y][x]; x++) if (w->g[y][x] == 'O' || w->g[y][x] == '[') acc += 100*y + x; return acc; } int main(int argc, char **argv) { static struct world w1,w2; int x,y, c; char *p; if (argc > 1) DISCARD(freopen(argv[1], "r", stdin)); for (y=0; fgets(w1.g[y], GW, stdin); y++) { if (!w1.g[y][0] || w1.g[y][0]=='\n') break; assert(y+1 < GH); assert(strlen(w1.g[y])*2+1 < GW); for (x=0; w1.g[y][x]; x++) if (w1.g[y][x] == 'O') { w2.g[y][x*2] = '['; w2.g[y][x*2+1] = ']'; } else { w2.g[y][x*2] = w1.g[y][x]; w2.g[y][x*2+1] = w1.g[y][x]; } if ((p = strchr(w1.g[y], '@'))) { w1.py = y; w1.px = p-w1.g[y]; w2.py = y; w2.px = w1.px*2; w1.g[w1.py][w1.px] = '.'; w2.g[w2.py][w2.px] = '.'; w2.g[w2.py][w2.px+1] = '.'; } } while ((c = getchar()) != EOF) switch (c) { case '^': move(&w1, 0,-1); move(&w2, 0,-1); break; case 'v': move(&w1, 0, 1); move(&w2, 0, 1); break; case '<': move(&w1,-1, 0); move(&w2,-1, 0); break; case '>': move(&w1, 1, 0); move(&w2, 1, 0); break; } printf("15: %d %d\n", score(&w1), score(&w2)); return 0; }
C
Solved part 1 without a grid, looked at part 2, almost spit out my coffee. Didn’t see that coming!
I used my visualisation mini-library to generate video with ffmpeg, stepped through it a bit, then thought better of it - this is a programming puzzle after all!
So I wrote a heuristic to find frames low on entropy (specifically: having many robots in the same line of column), where each record-breaking frame number was printed. That pointed right at the correct frame!
It was pretty slow though (.2 secs or such) because it required marking spots on a grid.
I noticed the Christmas tree was neatly tucked into a corner, concluded that wasn’t an accident, and rewrote the heuristic to check for a high concentration in a single quadrant.Reverted this because the tree-in-quadrant assumption proved incorrect for other inputs. Would’ve been cool though!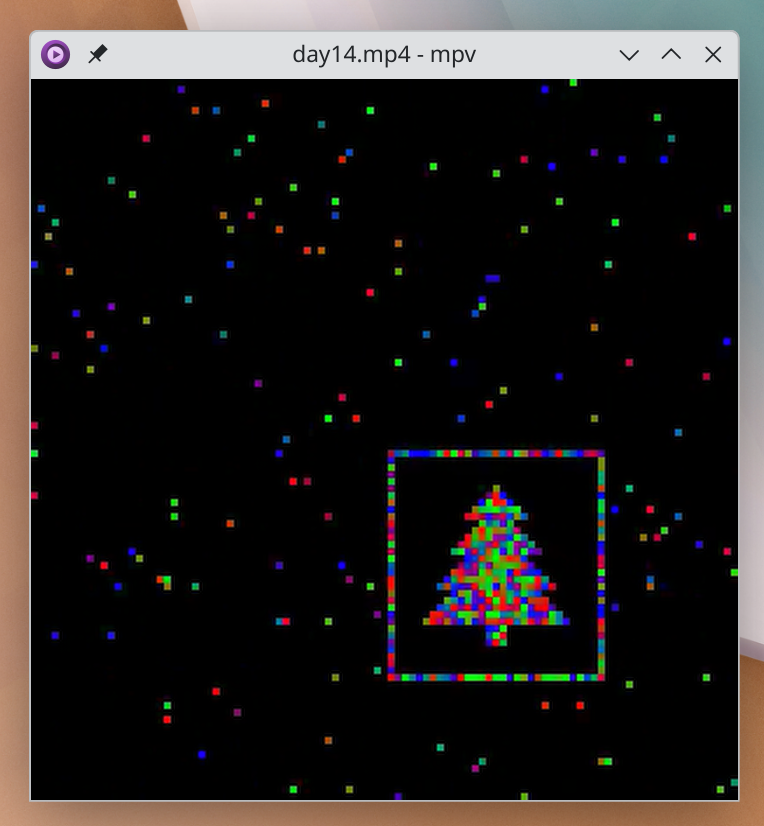
Code
#include "common.h" #define SAMPLE 0 #define GW (SAMPLE ? 11 : 101) #define GH (SAMPLE ? 7 : 103) #define NR 501 int main(int argc, char **argv) { static char g[GH][GW]; static int px[NR],py[NR], vx[NR],vy[NR]; int p1=0, n=0, sec, i, x,y, q[4]={}, run; if (argc > 1) DISCARD(freopen(argv[1], "r", stdin)); for (; scanf(" p=%d,%d v=%d,%d", px+n,py+n, vx+n,vy+n)==4; n++) assert(n+1 < NR); for (sec=1; !SAMPLE || sec <= 100; sec++) { memset(g, 0, sizeof(g)); memset(q, 0, sizeof(q)); for (i=0; i<n; i++) { px[i] = (px[i] + vx[i] + GW) % GW; py[i] = (py[i] + vy[i] + GH) % GH; g[py[i]][px[i]] = 1; if (sec == 100) { if (px[i] < GW/2) { if (py[i] < GH/2) q[0]++; else if (py[i] > GH/2) q[1]++; } else if (px[i] > GW/2) { if (py[i] < GH/2) q[2]++; else if (py[i] > GH/2) q[3]++; } } } if (sec == 100) p1 = q[0]*q[1]*q[2]*q[3]; for (y=0; y<GH; y++) for (x=0, run=0; x<GW; x++) if (!g[y][x]) run = 0; else if (++run >= 10) goto found_p2; } found_p2: printf("14: %d %d\n", p1, sec); return 0; }
C
Merry Christmas everyone!
Code
#include "common.h" int main(int argc, char **argv) { static char buf[7]; static short h[500][5]; /* heights */ static short iskey[500]; int p1=0, nh=0, i,j,k; if (argc > 1) DISCARD(freopen(argv[1], "r", stdin)); for (nh=0; !feof(stdin) && !ferror(stdin); nh++) { assert(nh < (int)LEN(h)); for (i=0; i<7; i++) { fgets(buf, 7, stdin); if (i==0) iskey[nh] = buf[0] == '#'; for (j=0; j<5; j++) h[nh][j] += buf[j] == '#'; } /* skip empty line */ fgets(buf, 7, stdin); } for (i=0; i<nh; i++) for (j=0; j<nh; j++) if (iskey[i] && !iskey[j]) { for (k=0; k<5 && h[i][k] + h[j][k] <= 7; k++) ; p1 += k == 5; } printf("25: %d\n", p1); return 0; }https://codeberg.org/sjmulder/aoc/src/branch/master/2024/c/day25.c
Made the 1 second challenge with most of it to spare! 😎